In bitcoin’s blockchain, a block of transactions is run through an algorithm to generate a hash, which is a string of numbers and letters that can be used to verify that a given set of data is the same as the original set of transactions, but not to obtain the original set of transactions. Bitcoin’s software does not run the entire block of transaction data—representing 10 minutes’ worth of transactions on average—through the hash function at one time, however.

Rather, each transaction is hashed, then each pair of transactions is concatenated and hashed together, and so on until there is one hash for the entire block. (If there is an odd number of transactions, one transaction is doubled and its hash is concatenated with itself.)

Visualized, this structure resembles a tree. In the diagram below, “T” designates a transaction, “H” a hash. Note that the image is highly simplified; an average block contains over 500 transactions, not eight.

Merkle Tree

Image by Julie Bang © Investopedia 2020

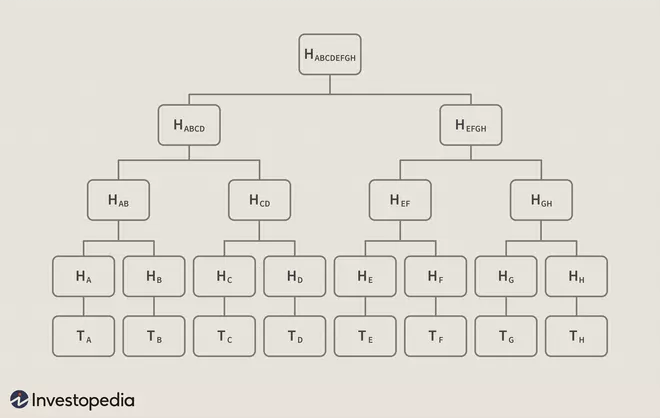
The hashes on the bottom row are referred to as “leaves,” the intermediate hashes as “branches,” and the hash at the top as the “root.” The Merkle root of a given block is stored in the header: for example, the Merkle root of block #482819 is e045b18e7a3d708d686717b4f44db2099aabcad9bebf968de5f7271b458f71c8. The root is combined with other information (the software version, the previous block’s hash, the timestamp, the difficulty target, and the nonce) and then run through a hash function to produce the block’s unique hash: 000000000000000000bfc767ef8bf28c42cbd4bdbafd9aa1b5c3c33c2b089594 in the case of block #482819. This hash is not actually included in the relevant block, but the next one; it is distinct from the Merkle root.

Merkle trees have three benefits:

• It provides a means to maintain the integrity and validity of data.
• It helps in saving the memory or disk space as the proofs, computationally easy and fast.
• Their proofs and management require tiny amounts of information to be transmitted across networks.

 

Use Cases for Merkle Trees

Merkle trees can be an integral part of the systems which require:

• Data verification
• Consistency verification
• Data Synchronization

So things like:

Cryptocurrencies

Many cryptocurrencies (including Bitcoin) store the transaction data in a merkle tree structure. Merkle trees help in consistency verification, i.e., making sure that the newer version of the ledger includes all the transactions from the previous version in the same order.

Version Control Systems

Version control systems like Git and Mercurial use specialized merkle trees to manage versions of files and even directories. One advantage of using merkle trees in version control systems is that we can simply compare hashes of files and directories between two commits to know if they’ve been modified or not, which is quite fast. 

Certificate Authorities

Certificate Authorities use merkle trees in their mechanisms to maintain certificate transparency logs that are verifiable. The log keeps on growing as new certificates are appended to it, and the transparency is verified using a log proof mechanism.

Database systems

No-SQL distributed database systems like Apache Cassandra and Amazon DynamoDB use merkle trees to detect inconsistencies between data replicas. This process of repairing the data by comparing all replicas and updating each one of them to the newest version is also called anti-entropy repair. 

Why are Merkle roots used in Bitcoin?

Merkle trees are essential in Bitcoin and many other cryptocurrencies. They’re an integral component of every block, where they can be found in the block headers. To get the leaves for our tree, we use the transaction hash of every transaction included in the block.

Mining

A Bitcoin block is made up of two pieces. The first part is the block header, a fixed-size segment containing metadata for the block. The second part is a list of transactions whose size is variable.

Miners need to continuously hash data to produce an output that matches certain conditions to mine a valid block. They can make many attempts before finding one. With each attempt, they change a random number in the block header to produce a different output. But much of the block remains the same. There can be hundreds and thousands of transactions, and you’d still need to hash them every time.

A Merkle root streamlines the process considerably. When you start mining, you line up all of the transactions you want to include and construct a Merkle tree. You put the resulting root hash (32 bytes) in the block header. Then, when you’re mining, you only need to hash the block header, instead of the whole block.

This works because it’s tamper-proof. You effectively summarize all of the block’s transactions in a compact format. You can’t find a valid block header and later change the transaction list, because that would change the Merkle root. When the block is sent to other nodes, they calculate the root from the transaction list. If it doesn’t match the one in the header, they reject the block.

Verification

There’s another interesting property of Merkle roots that we can leverage. This one concerns the light clients (nodes that don’t hold a full copy of the blockchain). If you’re running a node on a device with limited resources, you don’t want to download and hash all of a block’s transactions. What you can do instead is simply request a Merkle proof – evidence provided by the full node that proves that your transaction is in a particular block. 

Conclusion

Merkle trees have proven themselves highly useful in a range of computer science applications – as we’ve seen, they’re incredibly valuable in blockchains. In distributed systems, Merkle trees allow for easy verification of information without flooding the network with unnecessary data.

Without Merkle trees (and Merkle roots), Bitcoin and other cryptocurrencies’ blocks would not be nearly as compact as they are today. And while light clients are lacking on the privacy and security fronts, Merkle proofs enable users to check whether their transactions have been included in a block with minimal overhead.

For more details contact info@vafion.com

Follow us on Social media  : Twitter |  Facebook | Instagram | Linkedin

 

 

Similar Posts:

No similar blogs